Chapitre 6
Les EntitŽs Graphiques
2 - Maquettes virtuelles - Modles
2D
Le "2D" est une notion qui n'existe pas dans la rŽalitŽ. Travailler en 2D consiste ˆ limiter l'espace de travail ˆ un plan, gŽnŽralement horizontal. Ainsi les logiciels 2D imitent le travail d'un dessinateur sur une planche ˆ dessins ou une feuille de papier. Ces logiciels automatisent seulement le travail de Dessin et de Production de Plan. Ils ne fournissent aucun outil de crŽation dans l'espace. La notion d'Žchelle y est fondamentale et conduit trs souvent ˆ de graves imprŽcisions
2D 1/2
Le "2D 1/2" est une notion qui n'existe pas dans la rŽalitŽ. Travailler en 2D 1/2 consiste ˆ dessiner dans un plan des reprŽsentations perspectives en utilisant les moyens manuels du dessinateur. Un logiciel 2D ŽquipŽ d'un outil de reprŽsentation 2D 1/2 reste un logiciel 2D qui ne fournit aucun outil 3D.
3D
La "3D" est une technique de reprŽsentation de l'espace ˆ 3 dimensions, c'est ˆ dire du monde rŽel. La construction tridimensionnelle s'appelle "la modŽlisation".
La modŽlisation est essentiellement une activitŽ intellectuelle assistŽe par l'ordinateur. Il existe autant de manires de voir l'espace qu'il y a d'individus sur terre. Chacun dŽveloppe en effet sa propre manire de "comprendre" l'espace sous l'effet de l'Žducation reue et de sa propre culture. Certaines personnes n'arrivent pas ˆ "voir" en 3 dimensions.
La manire dont un EuropŽen et un Japonais conoivent l'espace est diamŽtralement opposŽe. Ceci se reflte clairement dans les types d'architectures et d'organisations de l'espace urbain par exemple.
Cette diversitŽ de la vision spatiale est une difficultŽ et un frein culturel ˆ l'utilisation des logiciels de 3 dimensions. Un exemple de ceci est l'hŽritage Žducatif de nombreuses personnes qui ont appris la reprŽsentation spatiale ˆ l'aide d'outils 2D (Plan/Coupe/Faade). Elles ont en gŽnŽral beaucoup de peine ˆ sortir de ce schŽma mental. Cette diversitŽ dans l'approche de l'espace s'appuie nŽanmoins sur une mŽthode universelle qui fournit les bases constructives de l'espace : la GŽomŽtrie Descriptive et la GŽomŽtrie Analytique. La GŽomŽtrie Descriptive et Analytique fournit les fondations communes sur lesquelles chacun peut dŽvelopper sa propre approche de l'espace.
3D Turbo est d'abord un logiciel 3D qui met en Ïuvre la GŽomŽtrie Descriptive et Analytique de manire puissante et conviviale pour permettre ˆ chacun de dŽvelopper sa propre vision de l'espace. 3D Turbo n'impose aucune mŽthode constructive particulire.
Bien entendu, la production de plans, qui est la base de l'activitŽ Žconomique de nombreuses entreprises, est un volet essentiel de 3D Turbo. En ce sens, 3D Turbo est Žgalement un logiciel 2D, c'est ˆ dire que ses outils de modŽlisation et son systme de visualisation perspective ou orthographique peuvent produire des dessins (au sens 2D) qui peuvent tre reproduits sur tout systme d'impression, donc produire des Plans.
L'usage du 2D est essentiellement facultatif. Il est possible de produire des ŽlŽments 3D ˆ partir d'ŽlŽments 2D et inversement.
On peut aussi concevoir directement en 3D en s'affranchissant des vieux schŽmas mentaux. A partir de lˆ, la crŽativitŽ de l'utilisateur peut s'exprimer en toute libertŽ, sans aucune contrainte.
La modŽlisation 3D produit des Maquettes virtuelles Žgalement appelŽes Modles. Ces maquettes sont stockŽes sous forme numŽrique dans l'ordinateur.
Elles sont construites en grandeur rŽelle. La notion d'Žchelle des logiciels 2D est remplacŽe en 3D par la notion de "niveau de dŽtail". Le niveau de dŽtail correspond ˆ la finesse (ou ˆ la grossiretŽ) de construction de la maquette virtuelle et conditionne pour beaucoup l'usage qui en sera fait.
S'il s'agit de reprŽsenter des b‰timents ˆ l'Žchelle d'une ville, il est probable qu'un niveau de dŽtail faible sera suffisant (type "Žpannelage").
S'il s'agit de reprŽsenter le b‰timent seul pour le mettre en valeur dans un rendu de concours, il est probable qu'il faille le modŽliser avec beaucoup de dŽtails.
|
|
|
Ci-dessus, une maquette virtuelle ˆ fort niveau de dŽtail |
|
|
|
Ci-dessus, une maquette virtuelle ˆ faible niveau de dŽtail |
La notion classique d'Žchelle reprend son sens lorsqu'on reprŽsente la maquette (le modle) dans une vue orthographique (dite aussi "vue plane" type plan, ŽlŽvation, coupe, faade). Il s'agit bien de reprŽsentations, de vues, de la maquette, obtenues par les dispositifs de visualisation du logiciel. C'est lˆ que rŽside toute la diffŽrence entre un "dessin" et un "modle". Un dessin n'est qu'une reprŽsentation (une vue) d'un modle.
Dans un logiciel 2D, comme ˆ la planche, on ne rŽalise que des dessins ˆ certaines Žchelles. Dans un logiciel 3D, on rŽalise des maquettes virtuelles 3D dont on produit des dessins par visualisation. Ces visualisations peuvent tre perspectives (coniques, axonomŽtriques, etc) ou planes associŽes ˆ une Žchelle de vue.
Les vues montrŽes prŽcŽdemment Žtaient des vues perspectives.
Toutes les vues ci-dessous ne sont que des vues orthographiques ˆ diverses Žchelles d'un seul et unique modle.
|
|
|
Žchelle 1/500
|
|
|
|
Žchelle 1/250
|
|
|
|
Žchelle 1/50
|
|
|
|
Žchelle 1/25
|
|
|
|
Žchelle 1/10
|
|
|
|
Žchelle 1/4 |
|
|
|
Žchelle 1/1 |
Ces vues peuvent tre enrichies par de la cotation, par des ŽlŽments graphiques (hachures, pochages, coloriages, etc).
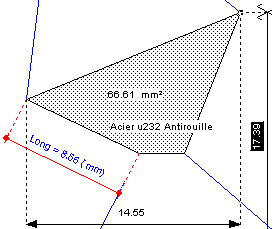
Elles peuvent tre :
á ImprimŽes sur tous les dispositifs d'impressions connus du systme (possŽdant un pilote installŽ),
á Mises en Page sur des planches de prŽsentation, avec le systme de Mise en Page intŽgrŽ ˆ 3D Turbo.
á ExportŽes sous divers formats (PDF, JPEG, TIFF, PNG, EPSF, DXF, etc.) et ˆ diverses Žchelles (jusquÕˆ 32765 x 32765 pixels) pour tre exploitŽes par d'autres logiciels de mise en page ou d'imagerie (Adobe Illustrator, PhotoShop, Xpress, PageMaker, Word, etc.).
Les EntitŽs Graphiques sont les ŽlŽments gŽomŽtriques ˆ partir desquels les modles 3D sont construits. Les entitŽs graphiques sont au nombre de sept :
- Les NÏuds
- Les Vecteurs
- Les Courbes
- Les Facettes
- Les Surfaces
- La Matire
- L'Espace
La modŽlisation dite "GŽomŽtrique" utilise les NÏuds, les Vecteurs, les Courbes et l'Espace.
La modŽlisation dite "Surfacique" utilise les Facettes et les Surfaces.
La modŽlisation dite "Volumique" utilise les Facettes, les Surfaces et la Matire.
3D Turbo est donc un modeleur GŽomŽtrique, Surfacique et Volumique. Les 3 mŽthodes de modŽlisation cohabitent harmonieusement et s'appuient l'une sur l'autre.
Les NÏuds ou Points 3D sont les entitŽs de base de 3D Turbo . Ce sont simplement des points de l'espace dŽfinis par un triplet de coordonnŽes (X,Y,Z) dans un repre CartŽsien.
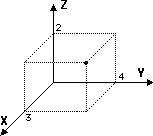
Point 3D - libre Point 3D - NÏud
Les points sont crŽŽs automatiquement ou semi-automatiquement dans toutes les fonctions de 3D Turbo. Les points peuvent Žgalement tre crŽŽs manuellement ou importŽs depuis des fichiers. On utilise aussi le terme NÏud lorsque ces points sont les extrŽmitŽs ou les points de rencontre de segments de droites. Dans ce manuel, les termes Points et NÏuds sont strictement Žquivalents et utilisŽs indiffŽremment. On parle aussi de Point Libre lorsque aucun segment n'aboutit ˆ ce point.
Se reporter au chapitre "Les NÏuds" pour conna”tre les fonctions sur les nÏuds.
Les vecteurs sont des segments de droite reliant 2 nÏuds. Ils sont thŽoriquement orientŽs, c'est ˆ dire qu'ils ont un nÏud "origine" et un nÏud "extrŽmitŽ". Cette notion d'orientation est trs importante et utilisŽe dans de nombreuses fonctions. Les vecteurs constituent l'ossature filaire des modles.
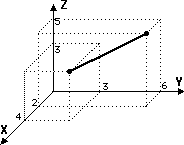
Se reporter au chapitre "Vecteurs, Droites et Segments de Droites" pour conna”tre les fonctions sur les vecteurs.
Les courbes sont des ŽlŽments mathŽmatiques basŽs sur les points appelŽs "p™les". Les p™les sont des points 3D, ce qui signifie que les courbes ne sont pas limitŽes ˆ un plan mais Žvoluent dans l'espace 3D. Il existe 3 sortes de courbes :
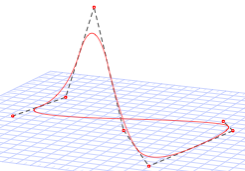
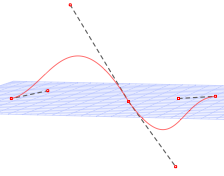
Les courbes Spline qui sont tendues par des P™les mais ne passent pas par les p™les. Elles peuvent tre ouvertes ou fermŽes. Elles sont tangentes aux points milieux des segments reliant les p™les :
|
|
|
|
|
|
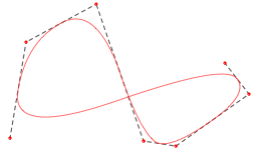
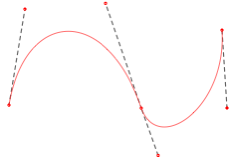
Les Courbes de BŽzier qui sont tendues par les tangentes aux p™les et passent par les p™les. Elles sont toujours ouvertes.
|
|
|
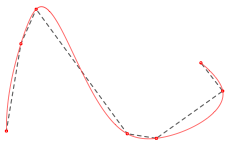
Les Courbes Tendues qui passent par les p™les. Elles peuvent tre ouvertes ou fermŽes.
|
|
|
Se reporter au chapitre "Les Courbes" pour conna”tre les fonctions sur les courbes.
Une facette est une surface plane dŽfinie par trois points ou plus (maximum 16384).
3D Turbo gŽnre automatiquement des facettes dans de nombreuses fonctions.
Les facettes doivent tre planes ou quasi planes. Des facettes gauches peuvent produire des erreurs dans les vues faces cachŽes et dans les opŽrations boolŽennes. Les facettes triangulaires sont Žvidemment automatiquement planes. Aussi, en cas de doute sur la planŽitŽ d'une face, il est possible de la subdiviser en facettes triangulaires (opŽration de "triangulation").
3D Turbo n'impose aucune contrainte sur la forme d'une facette (concavitŽ, convexitŽ, etc.).
Les facettes sont dotŽes de propriŽtŽs (couleur, orientation, transparence, etc.) qui permettent la visualisation des modles en mode faces cachŽes (dit aussi mode "Solide").
Se reporter au chapitre "Les Facettes" pour conna”tre les fonctions sur les facettes.
Une surface est une entitŽ mathŽmatique basŽe sur des points appelŽs "p™les". Une surface est toujours reprŽsentŽe par un maillage de facettes.
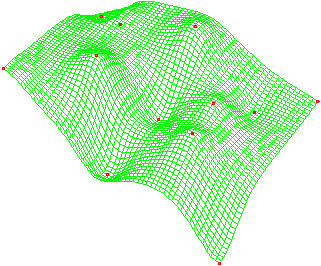
Se reporter au chapitre "Les GŽnŽrateurs de Surfaces 3D" pour conna”tre les fonctions sur les surfaces.
La matire correspond exactement ˆ la notion de volume solide plein ou vide. Elle permet de modŽliser en combinant 2 objets entre eux pour en crŽer un troisime par :
á Fusion
á Intersection
á Soustraction et d'autres fonctions
La "Matire" n'existe que par rapport ˆ "l'Antimatire", le "Plein" par rapport au "Vide", "l'IntŽrieur" par rapport ˆ "l'ExtŽrieur".
"Matire, Plein, IntŽrieur" sont des synonymes dŽsignant la partie solide d'un objet. "Antimatire, Vide, ExtŽrieur, Creux, Poche" sont des synonymes dŽsignant l'espace dŽpourvu de matire.
Se reporter au chapitre "Les OpŽrations sur la Matire et le Vide" pour conna”tre les fonctions sur la matire.
L'espace correspond au systme mathŽmatique qui contient et permet de reprŽsenter la gŽomŽtrie analytique et descriptive. On l'appelle espace cartŽsien. Lorsque l'espace est cartŽsien, il est rŽgi par un point origine (0,0,0) et un systme de 3 axes orthogonaux Ox, Oy, Oz.
Mais l'espace cartŽsien peut tre dŽformŽ, tordu, courbŽ, tirŽ, etc par diverses techniques.
La dŽformation de l'espace entra”ne la dŽformation des objets qu'il contient.
Ainsi, en modifiant localement et temporairement l'espace cartŽsien au voisinage d'un objet, on peut modifier la forme de cet objet. La modification de l'espace est donc une mŽthode de modŽlisation.